DSC 40B – Theoretical Foundations of Data Science II
Problems tagged with "depth first search"
Problem #111
Tags: depth first search, start and finish times
Suppose a depth-first search (DFS) is run on the graph shown below using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order of their label.
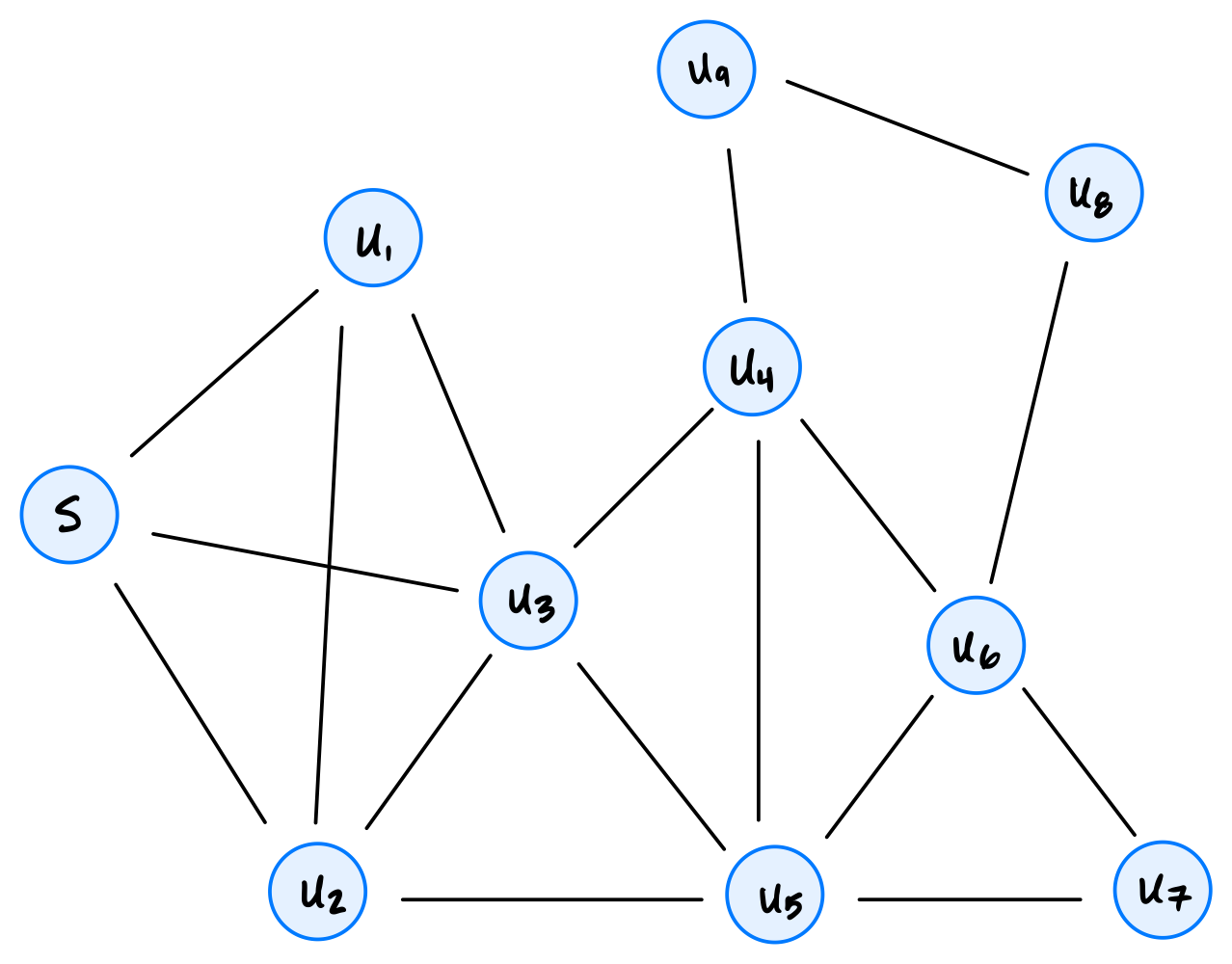
Part 1)
What will be the start time of node \(u_7\)?
Solution
8
Part 2)
What will be the finish time of node \(u_7\)?
Solution
9
Part 3)
Which node will be the DFS predecessor of node \(u_7\)?
Solution
\(u_6\)
Problem #112
Tags: depth first search, start and finish times
Let \(G\) be a graph, and suppose \(s\), \(u\), and \(v\) are three nodes in the graph.
Suppose a depth-first search (DFS) is run on \(G\) using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order by label. During this DFS, start and finish times are computed. Suppose it is found that:
Now suppose another DFS is run using node \(s\) as the source, but adopting a different convention about the order in which neighbors are produced. Suppose new_start and new_finish are the start and finish times found by this second DFS. True or False: it must be that
Solution
False.
Problem #114
Tags: depth first search
Suppose we define a forward-looking graph with \(n\) nodes to be the directed graph \(G = (V, E)\) with nodes \(u_1, \ldots, u_n\) and the edge \((u_i, u_j)\) if and only if \(i < j\). An example of such a graph with 4 nodes is shown below.
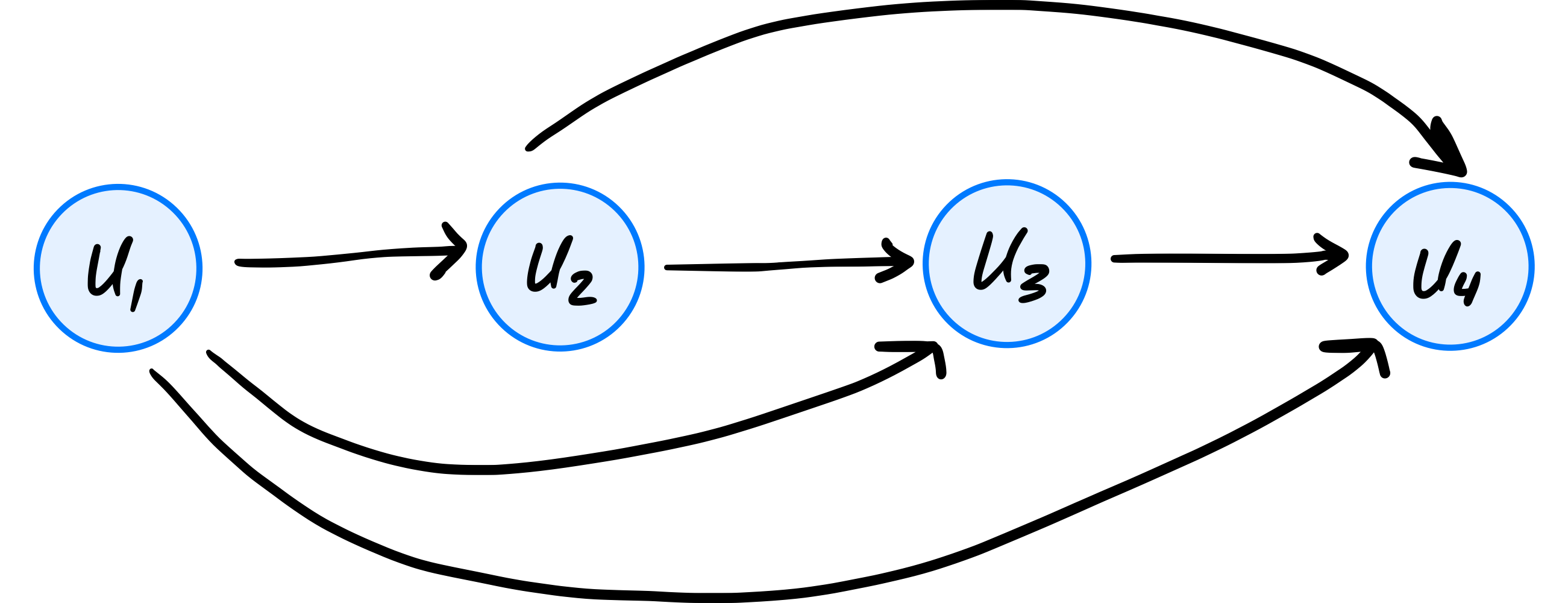
What is the time complexity of depth-first search when run on a forward-looking graph with \(n\) nodes, using node \(u_1\) as the source? State your answer as a function of \(n\) using asymptotic notation.
Solution
\(\Theta(n^2)\)
Problem #115
Tags: depth first search, aggregate analysis
Suppose an undirected graph \(G = (V, E)\) is a tree with 33 edges. Suppose a node \(s\) is used as the source of a depth-first search.
Including the root call of dfs on node \(s\), how many calls to dfs will be made?
Solution
34
Problem #116
Tags: depth first search, breadth first search
Let \(G = (V, E)\) be an undirected tree.
Suppose breadth-first search (BFS) and depth-first search (DFS) are each run on the graph using the same source node. True or False: for any node \(u\) in the graph, the BFS predecessor of \(u\) and the DFS predecessor of \(u\) must be the same.
Solution
True.
Problem #129
Tags: depth first search
Suppose a DFS is run on the graph shown below using node 11 as the source.
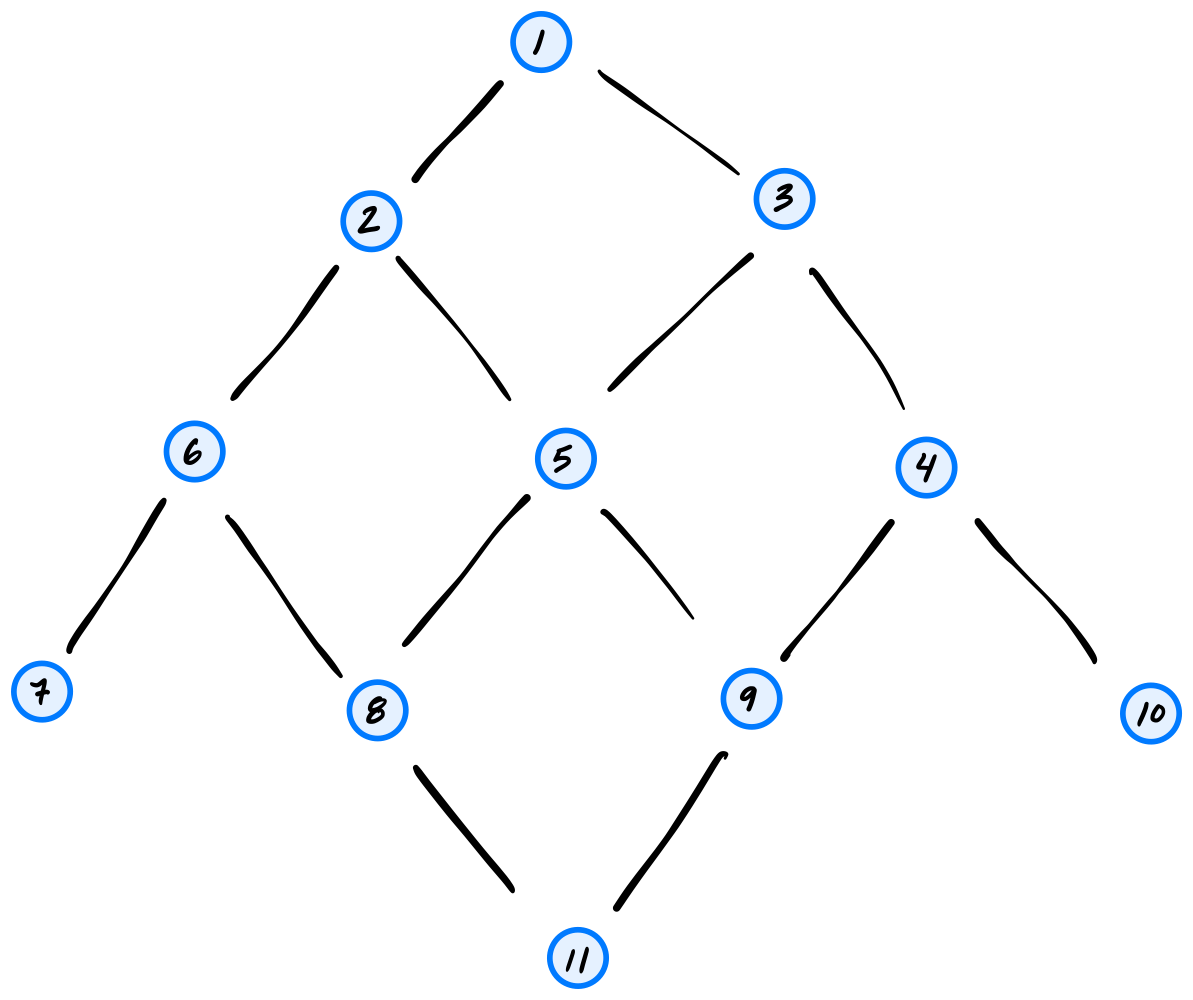
What will be the DFS predecessor of node 3 in the search? Use the convention that a node's neighbors are produced in ascending order by label.
Solution
1
Problem #130
Tags: depth first search, aggregate analysis
Consider the code shown below. It shows DFS as seen in lecture, with one modification: a print statement in the for-loop.
def dfs(graph, u, status=None):
"""Start a DFS at `u`."""
# initialize status if it was not passed
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[u] = 'pending'
for v in graph.neighbors(u):
print("Hello!")
if status[v] == 'undiscovered':
dfs(graph, v, status)
status[u] = 'visited'
How many times will "Hello!" be printed if dfs is run on the graph below using node \(u\) as the source? Note that dfs will not be restarted if the first call does not explore the whole graph.
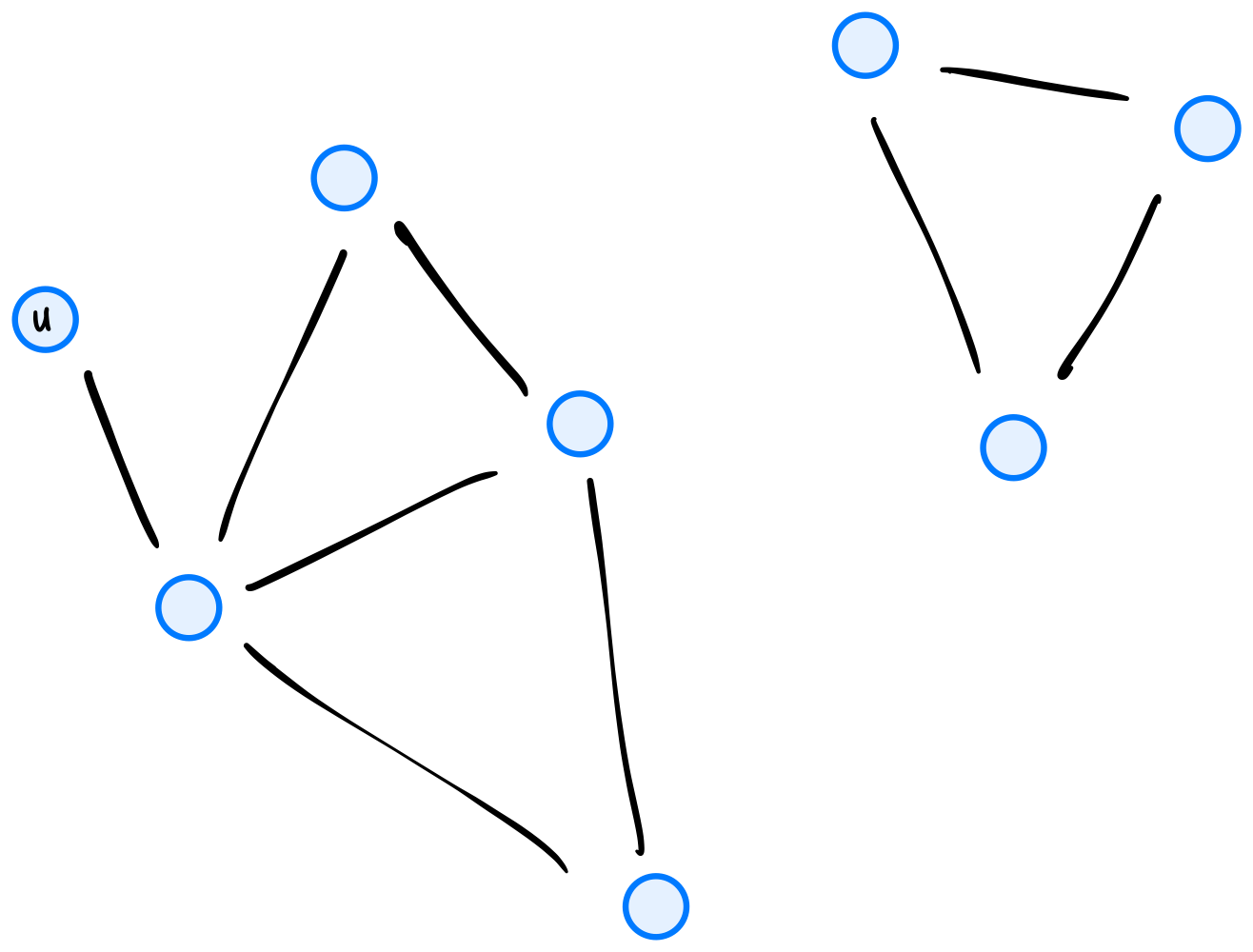
Solution
12
Problem #131
Tags: depth first search, start and finish times
Suppose again that a DFS is run on the graph shown in the above problem using node 11 as the source.
Part 1)
What will be the start time of node 2? Use the convention that the start time of the source is 1.
Solution
4
Part 2)
What will be the finish time of node 10?
Solution
11
Problem #132
Tags: depth first search, start and finish times
In a DFS on an undirected graph \(G\), the start time of node \(u\) is 12, while the finish time of node \(u\) is 37. How many nodes were marked pending between the moment that node \(u\) was marked pending and the moment that it was marked visited? Node \(u\) itself should be excluded from your count.
Solution
12
Problem #136
Tags: depth first search, breadth first search
Suppose both BFS and DFS are run on the same graph \(G = (V, E)\) using the same source node. Assume that \(G\) is a tree. Consider a particular node \(u\) in the graph. True or False: the BFS predecessor found for \(u\) and the DFS predecessor found for \(u\) must be the same.
Solution
True.
Problem #137
Tags: depth first search
Suppose a DFS is run on a directed graph. Let \(u\) and \(v\) be two nodes in the graph, and assume that the edge \((u, v)\) exists. True or False: it is possible that, at some moment in time, \(u\) is marked as ``visited'' while \(v\) is marked as ``undiscovered''.
Solution
False.
Problem #152
Tags: depth first search
Suppose a depth first search (DFS) is run on the graph shown below using node \(u_4\) as the source and the convention that graph.neighbors produces nodes in ascending order by label. What will be the predecessor of \(u_6\) in the DFS?

Solution
\(u_5\). DFS starts at \(u_4\), looks at the neighbors, and sees \(u_2\) is undiscovered, so it makes a recursive call dfs(u_2). At \(u_2\), it sees that \(u_1\) is undiscovered, and calls dfs(u_1). At \(u_1\), there's nothing to do, so it's marked as visited and the recursion unrolls back to the call on dfs(u_2). We then look at the next neighbor of \(u_2\), which is \(u_3\). We make a call to dfs(u_3), which looks at its neighbors and sees \(u_5\). We make a call to dfs(u_5), and during this call we discover \(u_6\), meaning that \(u_5\) is the DFS predecessor of \(u_6\).
Problem #156
Tags: depth first search, trees
What is the time complexity of depth first search (DFS) when run on a tree with \(n\) nodes?
Solution
\(\Theta(n)\)
Problem #157
Tags: depth first search
Suppose a depth first search is run on a directed graph. True or False: it is possible that, at any moment in time, there is a node marked as visited which has a neighbor (successor) that is marked as pending.
Solution
True
Problem #158
Tags: depth first search, start and finish times
Suppose a depth first search is run on the graph shown below using node \(u_4\) as the source, and adopt the convention that graph.neighbors produces nodes in ascending order of label. Which node will have the smallest finish time?

Solution
\(u_1\)
Problem #159
Tags: depth first search, start and finish times
Suppose a depth first search is run on the graph shown below using node \(u_4\) as the source, and adopt the convention that graph.neighbors produces nodes in ascending order of label. What will be the start time of node \(u_7\)?

Solution
12
Problem #161
Tags: depth first search, start and finish times
Suppose \(T = (V, E)\) is a connected, undirected graph with no cycles (that is, \(T\) is a tree). Suppose a depth first search is run on \(T\) using node s as the source. Assume that node s has two neighbors: \(u\) and \(v\). If \(|V| = 15\), which one of the below represents possible start and finish times of \(u\) and \(v\)? You may assume that graph.neighbors produces neighbors in ascending order of label.
Solution
start[u] = 2, finish[u] = 21, start[v] = 22, finish[v] = 29
Problem #213
Tags: depth first search
A modification of the dfs function from lecture is shown below. It is the same as the original dfs function, except that it has an added print statement.
def dfs(graph, u, status=None):
"""Start a DFS at `u`."""
# initialize status if it was not passed
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[u] = 'pending'
for v in graph.neighbors(u):
print("Hello!")
if status[v] == 'undiscovered':
dfs(graph, v, status)
status[u] = 'visited'
Consider running this algorithm on the following graph, starting at node \(a\):
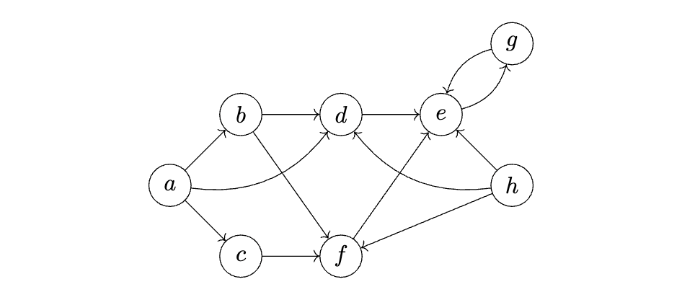
How many times will "Hello!" be printed? Note that this is not a full DFS, and that not all nodes are reachable from \(a\).
Problem #214
Tags: depth first search
True or False: a depth first search with source node \(s\) is guaranteed to find the longest simple path starting from \(s\) in a connected, undirected graph \(G\) That is, suppose that there is a unique longest simple path in \(G\), and call this path \(p\). True or False: the longest simple path in the DFS forest must be also be \(p\).
Solution
False
Problem #216
Tags: depth first search
Suppose a depth first search (DFS) is run on the graph below, starting at node \(a\). Start and finish times are calculated using the convention that the start time of node \(a\) is 1.
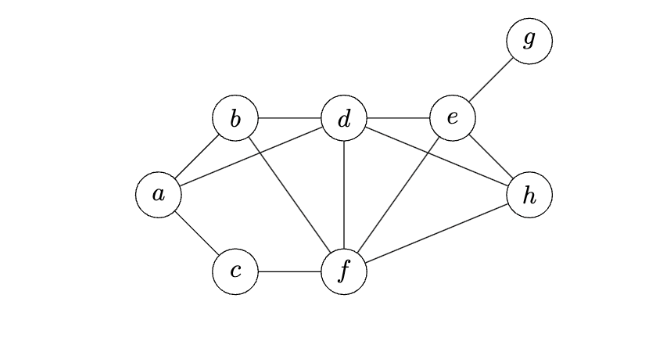
What will be the finish time of node \(e\)? Assume the convention that a node's neighbors are produced in alphabetical order.
Problem #217
Tags: depth first search
Suppose that a depth first search is being performed on an undirected graph, and when dfs is called on a node \(u\), the statuses of all of its neighbors are printed. True or False: it is possible that one of the neighbors is marked as ``visited''.
Solution
False
Problem #238
Tags: depth first search
A modification of the dfs function from lecture is shown below. It is the same as the original dfs function, except that it has an added print statement.
def dfs(graph, u, status=None):
"""Start a DFS at `u`."""
# initialize status if it was not passed
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[u] = 'pending'
for v in graph.neighbors(u):
if status[v] == 'undiscovered':
print("Hello!")
dfs(graph, v, status)
status[u] = 'visited'
Consider running this algorithm on the following graph, starting at node \(a\):
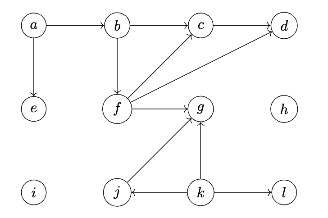
How many times will "Hello!" be printed? Note that this is not a full DFS, and that not all nodes are reachable from \(a\).
Problem #240
Tags: depth first search
Suppose that a depth first search is being performed on an undirected graph, and when dfs is called on a node \(u\), the statuses of all of its neighbors are printed. True or False: it is possible that one of the neighbors is marked as ``visited''.
Solution
False
Problem #249
Tags: depth first search
Suppose a depth first search (DFS) is run on the graph below, starting at node \(a\). Start and finish times are calculated using the convention that the start time of node \(a\) is 1.
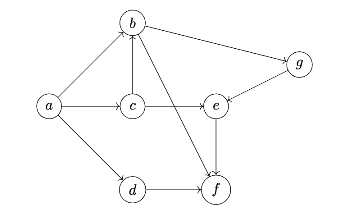
What will be the finish time of node \(c\)? Assume the convention that a node's neighbors are produced in alphabetical order.